| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Asteroid RL
- 소행성
- dictionary
- cURL
- 미분 방정식
- 계단 오르기
- 자바
- BST
- 딕셔너리
- 회로이론
- 선적분
- 강화학습
- 파이썬
- 신경망
- 벡터해석
- 최단 경로
- Class
- 코드업
- 함수
- 이진탐색트리
- 자료형
- 피보나치 수열
- 델
- 딥러닝
- 백트래킹
- java
- auto-encoder
- 벡터 해석
- Python
- 2P1L
- Today
- Total
Zeta Oph's Study
[천체 역학] 조석력 (Tidal Force) 본문
이 글에서는 조석력에 대해 알아보겠습니다.
바닷가에서 밀물과 썰물을 보신 적이 있을 것입니다. 바닷물이 많이 차올랐다가, 빠졌다가를 반복하죠. 이러한 현상을 우리는 조석(tide)이라고 합니다. 이 조석을 일으키는 힘이 바로 조석력(tidal force)입니다.
조석력은 사실 우리가 이미 알고 있는 만유인력의 또 다른 형태입니다. 만유인력은 아래와 같이 주어지죠.
$$\mathbf{F}_G=-\frac{Gm_1m_2}{r^2}\hat{\mathbf{r}}$$
식의 형태를 보시면, 거리의 제곱에 반비례 하는 것을 알 수 있습니다. 조석력은 이러한 거리에 따라 크기가 변하는 만유인력의 성질과 물체의 크기 때문에 나타나는 현상이라고 할 수 있습니다.

달과 지구를 생각해봅시다. 지구는 크기가 있는 물체이므로, 달에 가까운 부분(1), 지구 중심(2), 달에 먼 부분(3)에 작용하는 만유인력이 모두 다를 것입니다.
따라서 지구 중심의 좌표계에서 보면, (1)과 (3)에 지구 중심으로부터 멀어지는 힘이 작용하는 것처럼 보이게 되죠. 이러한 힘이 조석력입니다. 즉, 달에서 가까운 부분은 달 쪽으로, 달에서 먼 부분은 달 반대쪽으로 조석력이 작용하게 됩니다.
조석력 유도
조석력을 정성적으로 이해해보았으니, 이제 조석력에 대한 수식을 정량적으로 유도해봅시다.
지구와 달에 작용하는 상황을 생각하여 조석력에 대한 식을 유도할 건데, 몇가지 간단한 가정을 합시다.
1. 지구와 달은 균일한 강체 구이고, 지구는 완전히 물로 덮여 있습니다.
2. 오직 달에 의한 조석력만 고려합니다. (태양의 조석력은 고려하지 않습니다)
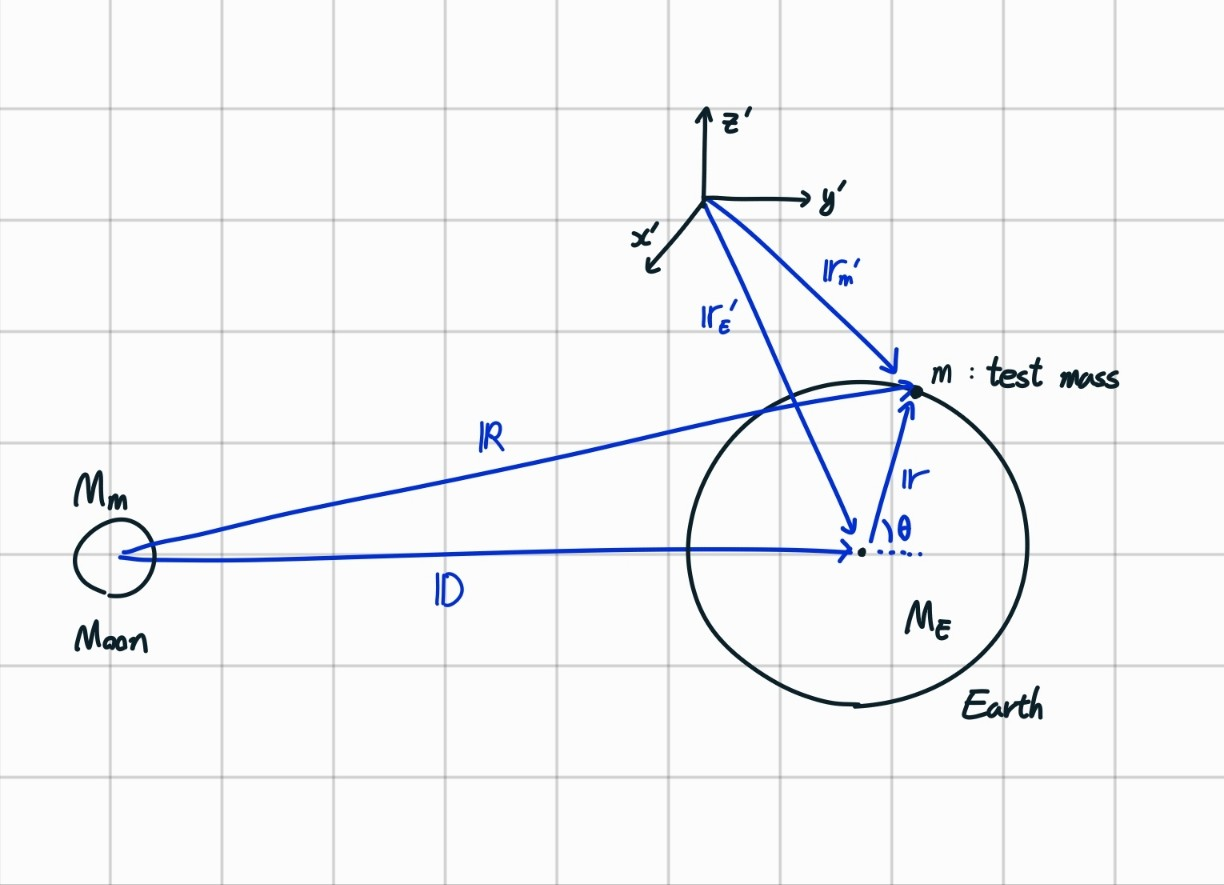
위 그림과 같이, 지구의 질량을 $M_E$, 달의 질량을 $M_m$, 지구 표면에 있는 test mass의 질량을 $m$이라 합시다. 달의 중심을 원점으로 하는 지구 중심, test mass의 위치 벡터는 각각 $\mathbf{R}$, $\mathbf{D}$이고, 지구 중심을 원점으로 하는 test mass의 위치 벡터는 $\mathbf{r}$입니다.
또한 지구는 달의 중력에 의해 가속되는 비관성계입니다. 따라서 관성력까지 고려해주어야 올바른 유도를 할 수 있습니다.지구 밖의 관찰자(관성 좌표계)를 잡고, 그 좌표계를 기준으로 지구와 test mass의 위치 벡터를 각각 $\mathbf{r}^{'}_{E}$, $\mathbf{r}^{'}_{m}$이라고 합시다.
관성 좌표계에서 test mass와 지구에 대해 운동방정식을 쓰면 아래 두 식과 같습니다.
$$m\mathbf{\ddot{r}}^{'}_m=-\frac{GmM_E}{r^2}\hat{\mathbf{r}}-\frac{GmM_m}{R^2}\hat{\mathbf{R}}$$
$$M_E\mathbf{\ddot{r}}^{'}_E=-\frac{GM_EM_m}{D^2}\hat{\mathbf{D}}$$
각 식을 질량으로 나누어 가속도의 형태로 정리해주면,
$$\mathbf{\ddot{r}}^{'}_m=-\frac{GM_E}{r^2}\hat{\mathbf{r}}-\frac{GM_m}{R^2}\hat{\mathbf{R}}$$
$$\mathbf{\ddot{r}}^{'}_E=-\frac{GM_m}{D^2}\hat{\mathbf{D}}$$
이고, 이를 이용하여 지구-달 계(비관성계)에서 test mass가 받는 가속도를 쓸 수 있습니다. 관성계에서 본 test mass가 받는 가속도에서 관성력에 해당하는 가속도를 빼주면 되죠. 이때 test mass는 지구 위에 있으므로 이 상황에서 관성력은 지구가 받는 힘이 될 것입니다.
따라서 관성계에서 test mass의 가속도는,
$$\mathbf{\ddot{r}}^{'}=\mathbf{\ddot{r}}^{'}_m-\mathbf{\ddot{r}}^{'}_E\\=-\frac{GM_E}{r^2}\mathbf{\hat{r}}-\frac{GM_m}{R^2}\mathbf{\hat{R}}+\frac{GM_m}{D^2}\mathbf{\hat{D}}\\=-\frac{GM_E}{r^2}\mathbf{\hat{r}}-GM_m(\frac{\mathbf{\hat{R}}}{R^2}-\frac{\mathbf{\hat{D}}}{D^2})$$
입니다.
식을 살펴봅시다. $-\frac{GM_E}{r^2}\mathbf{\hat{r}}$ 항은, 지구의 중력에 의한 가속도를 나타낸다는 것을 쉽게 알 수 있습니다. 그렇다면 뒤의 $-GM_m(\frac{\mathbf{\hat{R}}}{R^2}-\frac{\mathbf{\hat{D}}}{D^2})$ 항은 무엇을 의미할까요? 바로 이 항들이 조석력에 의한 가속도를 나타내는 항입니다. 따라서 조석력 $\mathbf{F_T}$를 아래와 같이 써줄 수 있습니다.
$$\mathbf{F_T}=-GmM_m(\frac{\mathbf{\hat{R}}}{R^2}-\frac{\mathbf{\hat{D}}}{D^2})$$
조석력을 표현하는 식을 얻었으니, 이제 이 식을 사용하기 편하게 정리해봅시다. 아래 그림과 같이 test mass의 위도를 $\theta$로 표시하고, 새로운 , $xy$좌표계를 설정하여 조석력을 $\mathbf{F_T}=F_{Tx}\mathbf{\hat{i}}+F_{Ty}\mathbf{\hat{j}}$와 같이 $x$, $y$성분 별로 나타내 보겠습니다.

먼저 $D, R >> r$이라고 가정해줍니다. 위의 식을 정리하면,
$$\mathbf{F_T}=-GmM_m(\frac{\mathbf{\hat{R}}}{R^2}-\frac{\mathbf{\hat{D}}}{D^2})\\=-GmM_m(\frac{\mathbf{R}}{R^3}-\frac{\mathbf{D}}{D^3})\\=-GmM_m(\frac{(D+r\cos\theta)\hat{\mathbf{i}}+r\sin\theta\hat{\mathbf{j}}}{R^3}-\frac{D\hat{\mathbf{i}}}{D^3})\\=-GmM_m(\frac{D+r\cos\theta}{R^3}-\frac{1}{D^2})\hat{\mathbf{i}}-GmM_m\frac{r\sin\theta}{R^3}$$
여기서 제2 코사인 법칙에 의해,
$$R^2=D^2+r^2-2Dr\cos(\pi-\theta)\\=D^2(1+(\frac{r}{D})^2+2\frac{r}{D}\cos\theta)$$
이때 $\frac{r}{D}<<1$이므로,
$$R^2\approx D^2+2Dr\cos\theta$$
$$R^3=(D^2+2Dr\cos\theta)^{\frac{3}{2}}=D^3(1+2\frac{r}{D}\cos\theta)^{\frac{3}{2}}$$
테일러 근사 $(1+x)^n\approx1+nx (x<<1)$을 사용하여
$$R^3=D^3(1+3\frac{r}{D}\cos\theta)$$
이를 이용하여 $F_{Tx}$를 아래와 같은 과정을 통해 정리할 수 있습니다.
$$F_{Tx}=-GmM_m(\frac{D+r\cos\theta}{R^3}-\frac{1}{D^2})\\ \approx -\frac{GmM_m}{D^2}(\frac{D+r\cos\theta}{D+3r\cos\theta}-1)\\=-\frac{GmM_m}{D^2}\frac{-2r\cos\theta}{D+3r\cos\theta}\\ \approx \frac{2GmM_mr\cos\theta}{D^3}$$
같은 방식으로, $F_{Ty}$ 또한 근사를 통해 정리하면,
$$F_{Ty} \approx -\frac{GmM_mr\sin\theta}{D^3}$$
따라서 결론적으로 조석력 식을 아래와 같이 쓸 수 있습니다.
$$\mathbf{F_T}=\frac{2GmM_mr\cos\theta}{D^3}\mathbf{\hat{i}}-\frac{GmM_mr\sin\theta}{D^3}\mathbf{\hat{j}}$$
조수 간만의 차 계산
조석력으로 인해 만조와 간조가 번갈아 가며 나타나게 되는데, 이때 만조와 간조의 높이 차를 조수 간만의 차라고 합니다. 이 높이차를 위에서 구한 조석력을 이용하여 직접 계산해봅시다.

지구의 자전으로 달의 위치가 90도 변화하면 한 위치에서 간조에서 만조로 바뀌는 것을 상상해볼 수 있습니다. 실제로는 지구의 자전으로 인해 움직이는 것이지만, 위 그림에서는 편의상 달을 고정시키고 test mass m이 움직이는 것으로 나타내었습니다.
test mass의 위치를 지구 중심을 원점으로 하는 좌표계 $(x, y)$로 나타낼 수 있고, 이를 이용하여 조석력을 다시 쓸 수 있습니다.
$$\mathbf{F_T}=\frac{2GmM_mx}{D^3}\mathbf{\hat{i}}-\frac{GmM_my}{D^3}\mathbf{\hat{j}}$$
조석력이 한 일을 구해봅시다. 일은 힘을 이동 거리로 적분한 것으로 쓸 수 있고, 위 그림에서 $x$좌표는 $0$에서 $r$로, $y$좌표는 $r$에서 $0$으로 변화하였습니다. 따라서 조석력이 한 일은
$$W=W_x+W_y=\int_{0}^{r}F_{Tx}dx+\int_{r}^{0}F_{Ty}dy\\=\int_{0}^{r}\frac{2GmM_mx}{D^3}dx+\int_{r}^{0}-\frac{GmM_my}{D^3}dy\\=\frac{3GmM_mr^2}{2D^3}$$
이고, 조석력이 한 일과 퍼텐셜 에너지 변화량 $mgh$가 같다는 것을 이용하여 해수면 높이차 $h$를 계산할 수 있습니다.
$$h=\frac{3GM_mr^2}{2gD^3}\\=\frac{3\cdot(6.67\cdot10^{-11} kg^{-1}m^3s^{-2})\cdot(7.36\cdot10^{22} kg)\cdot(6378 km)^2}{2\cdot(9.81 ms^{-2})\cdot(384400 km)^3}\\ \approx0.54m$$
이렇게 이 글에서는 조석력의 유도와 이를 활용하여 조수 간만의 차를 구하는 과정을 다루어 보았습니다. 다음 번에는 이 조석력과 연관지어 위성이 조석력을 견디지 못하고 찢어지는 한계인 로슈 한계에 대해 알아보도록 하겠습니다.
'천문학' 카테고리의 다른 글
| [관측] 10월 29일 부분월식 (2) | 2023.10.29 |
|---|

