| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Asteroid RL
- 자료형
- 2P1L
- 소행성
- 함수
- Python
- 회로이론
- BST
- cURL
- 강화학습
- 벡터해석
- dictionary
- java
- 자바
- 벡터 해석
- 코드업
- 계단 오르기
- 미분 방정식
- 신경망
- auto-encoder
- 백트래킹
- 최단 경로
- 딕셔너리
- 델
- 파이썬
- Class
- 딥러닝
- 선적분
- 이진탐색트리
- 피보나치 수열
- Today
- Total
Zeta Oph's Study
[Data Structure (Java)] Hash (Separate Chaining & Linear Probing) 본문
[Data Structure (Java)] Hash (Separate Chaining & Linear Probing)
Zeta Oph 2024. 6. 5. 17:54
https://crane206265.tistory.com/87
[Data Structure (Java)] Map ADT
https://crane206265.tistory.com/86 [Data Structure (Java)] Heapsorthttps://crane206265.tistory.com/85 [Data Structure (Java)] Heaphttps://crane206265.tistory.com/84 [Data Structure (Java)] Tree (3) - Binary Search Treehttps://crane206265.tistory.com/82
crane206265.tistory.com
이번에는 Hash를 다루어 보겠습니다. 개인적으로 제일 흥미로웠던 것 같아요.
Hash Function
: functions that maps data of arbitrary size to fixed-size values
(function that computes array index from key)
--> transforms the search key to index in [0, N-1]
Hash(Hash Value / Hash Code) : output of hash function
2 Parts of Hashing
1. hash code that maps a key k to an integer
2. a compression function that maps the hash code to an array index (integer in [0, N-1])
<Properties of Hash Function>
| - | Explanation |
| Required Properties (for correctness) |
deterministic : equal keys must produce the same hash value |
| each key hases to index in [0, N-1] | |
| Desirable Properties (for performance) |
efficient to compute |
| uniform hashing assumption : (uniformly & independently distributed keys into array indicies) |
collision : 2 distinct keys that hash to same index
--> hash function that avoids collisions : desirable
Hashing Part 1. hashCode() : Mapping a Key to an Integer
all java classes inherit a method hashCode() : returns a 32-bit integer
required x.equals(y) ==> x.hashCode() == y.hashCode() highly desirable !x.equals(y) ==> x.hashCode() != y.hashCode()
ex) for String data type
Horner's Method : hash string of length L
with some L-1 deg polynomial (below)
$h = s[0]\cdot31^{L-1} + s[1]\cdot31^{L-2}+\cdots+s[L-1]\cdot31^0$
* s[i] : character's ASCII
Hashing Part 2. Compression Function : hashCode to integer in [0, N-1]
hash code : int in $[-2^31, 2^31-1]$
compression functions : maps to int in [0, N-1]
--> division method : i mod N
(taking N to be a prime number -> "spread out" the distribution of hashed values)
Compression Function Operation Result x.hashCode()%N bug with negative integer Math.abs(x.hashCode())%N overflow at -2^31 --> bug occurs (x.hashCode() & 0x7fffffff)%N turn the 32-bit integer into 31-bit non-negative integer -> mod operator
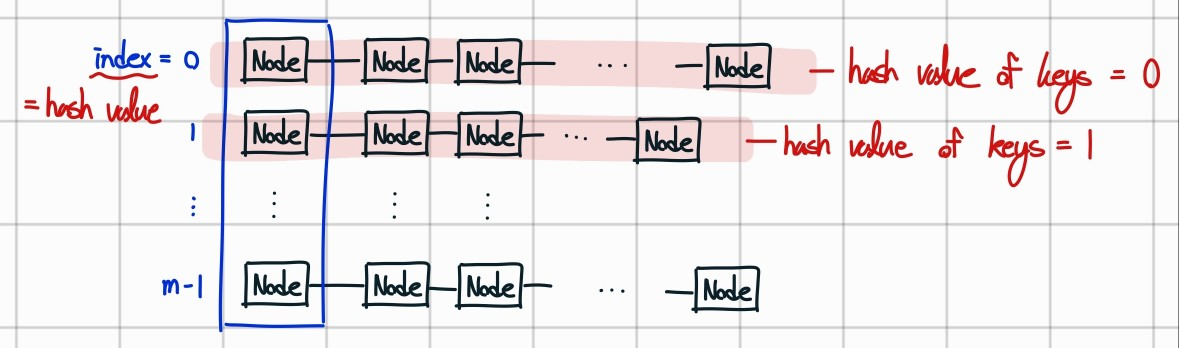
Hash Table : Separate Chaining
: way to resolve the collision
Bulid a linked list for each of positions in array for hash values
==> Operations
- hash : map key to table index i in [0, m-1]
- insert : add key-value pair at front of chain i
- search : scan only chain corresponding to its hash value
--> perform sequential search only in chain i
load factor of a hash table
n : # of key-value pairs
m : # of lists ( == the size of array)
avg # of elements stored in a list : load factor $\mathbf{\alpha=\frac{n}{m}}$
with uniform hashing assumption, $\text{# of compares} \propto \text{load factor } \alpha$
$n = O(m) \Rightarrow \alpha=\frac{n}{m}=O(1)$
$\therefore$ running time of searching / inserting : $\mathbf{O(1)}$ (linear time)
Separating Chain Implementation
@SuppressWarnings("unchecked")
public class SeparatingChainHash<Key, Value> {
//----- constructor & instance variable -----
private int n;
private int m;
private Node[] st;
private static class Node {
private Object key;
private Object val;
private Node next;
public Node(Object key, Object val, Node next) {
this.key = key;
this.val = val;
this.next = next;
}
}
public SeparatingChainHash() {
this(997);
}
public SeparatingChainHash(int m) {
this.m = m;
st = new Node[m];
}
//----- methods -----
public int size() {
return n;
}
public boolean isEmpty() {
return n==0;
}
public boolean contains(Key key) {
return get(key) != null;
}
public Value get(Key key) {
int i = hash(key);
for(Node x = st[i]; x != null; x = x.next) {
if(key.equals(x.key)) return (Value) x.val;
}
return null;
}
public void put(Key key, Value val) {
if(val == null) {
delete(key);
return;
}
int i = hash(key);
for(Node x = st[i]; x != null; x = x.next) {
if(key.equals(x.key)) {
x.val = val;
return;
}
}
n++;
st[i] = new Node(key, val, st[i]);
}
public Object delete(Key key) {
int i = hash(key);
if(key.equals(st[i].key)) return delete(st[i]);
for(Node x = st[i]; x.next != null; x = x.next) {
if(key.equals(x.next.key)) return delete(x.next);
}
return null;
}
private Object delete(Node x) {
Node temp = x;
Object res = temp.val;
x = temp.next;
temp = null;
n--;
return res;
}
//----- helper methods -----
private int hash(Key key) {
return (key.hashCode() & 0x7fffffff) % m;
}
}Hash Table : Linear Probing
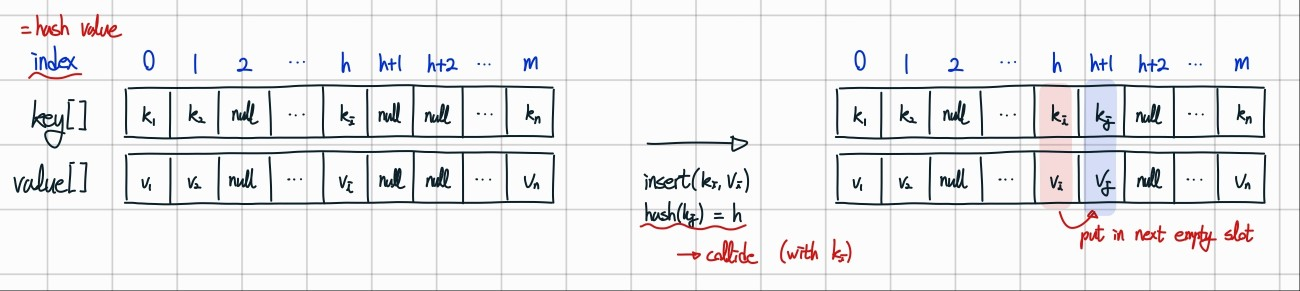
Linear Probing
key-value pairs in 2 parallel arrays
use empty place of the arrays
: when a new key collides, find next empty slot, and put it there
==> array size M must be greater than # of key-value pairs N (hash value is in [0, M-1])
==> dynamic array is necessary : need to use resize()
- search : start from the hash value, search until finding the key or an unused cell
* if next slot is out of range -> go to first of array
load factor of a hash table
n : # of key-value pairs
m : the size of a hash table ($m \geq n$ to have empty space)
avg % of table entries that are occupied : load factor $\mathbf{\alpha=\frac{n}{m}}$
($m \geq n, \Rightarrow \alpha=\frac{n}{m}\geq1$)
with uniform hashing assumption, $\text{# of compares} \propto \text{load factor } \alpha$
$n = O(m) \Rightarrow \alpha=\frac{n}{m}=O(1)$
$\therefore$ running time of searching / inserting : $\mathbf{O(1)}$ (linear time)
Linear Probing Implementation
public class LinearProbingHash<Key, Value> {
//----- constructor & instance variables -----
private static final int INIT_CAPACITY = 4;
private Key[] keys;
private Value[] vals;
private int m;
private int n;
public LinearProbingHash() {
this(INIT_CAPACITY);
}
@SuppressWarnings("unchecked")
public LinearProbingHash(int capacity) {
m = capacity;
n = 0;
keys = (Key[]) new Object[m];
vals = (Value[]) new Object[m];
}
//----- methods -----
public int size() {
return n;
}
public boolean isEmpty() {
return n == 0;
}
public boolean contains(Key key) {
return get(key) != null;
}
public Value get(Key key) {
for(int i = hash(key); keys[i] != null; i = (i+1)%m)
if(key.equals(keys[i])) return vals[i];
return null;
}
public void put(Key key, Value val) {
if(n >= m/2) resize(2*m);
int i;
for(i = hash(key); keys[i] != null; i = (i+1)%m) {
if(key.equals(keys[i])) {
vals[i] = val;
return;
}
}
keys[i] = key;
vals[i] = val;
n++;
}
public Value delete(Key key) {
Value res;
int i;
for(i = hash(key); true; i = (i+1)%m) {
if(key.equals(keys[i])) {
res = vals[i];
break;
}
if(keys[i] == null) {
res = null;
break;
}
}
keys[i] = null;
vals[i] = null;
n--;
if(n <= m/4) resize(m/2);
return res;
}
//------ helper methods -----
private void resize(int capacity) {
LinearProbingHash<Key, Value> temp = new LinearProbingHash<Key, Value>(capacity);
for(int i = 0; i < m; i++) {
if(keys[i] != null) {
temp.put(keys[i], vals[i]);
}
}
keys = temp.keys;
vals = temp.vals;
m = temp.m;
}
private int hash(Key key) {
return (key.hashCode() & 0x7fffffff) % m;
}
}Hash Table : Running Time Summary
Hash table - under uniform hashing assumption
: constant avg. running time
but
: need good hash function
: ordered map operation are not easily supported
| Implementation | Worst Case | Average Case | ||
| search | insert | search | insert | |
| Separate Chaning (array of lists) |
O(n) | O(n) | O(1)* | O(1)* |
| Linear Probing (parallel arrays) |
O(n) | O(n) | O(1)* | O(1)* |
| Sequential Search (unordered list) |
O(n) | O(n) | O(n) | O(n) |
| Binary Search (ordered array) |
O(log n) | O(n) | O(log n) | O(n) |
* under uniform hashing assumption
'프로그래밍 > Java' 카테고리의 다른 글
| [Data Structrue (Java)] Tree (4) - Binary Search Tree Map (1) | 2024.06.06 |
|---|---|
| [Data Structure (Java)] Set (1) | 2024.06.05 |
| [Data Structure (Java)] Map (1) | 2024.06.03 |
| [Data Structure (Java)] Heapsort (2) | 2024.06.03 |
| [Data Structure (Java)] Heap (2) | 2024.06.02 |
