| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 백트래킹
- 피보나치 수열
- 미분 방정식
- 선적분
- 자료형
- auto-encoder
- 델
- cURL
- 딕셔너리
- 코드업
- Asteroid RL
- Class
- BST
- 딥러닝
- 계단 오르기
- 함수
- 신경망
- 최단 경로
- 강화학습
- 자바
- 이진탐색트리
- 벡터 해석
- 회로이론
- 소행성
- 파이썬
- Python
- 2P1L
- dictionary
- 벡터해석
- java
- Today
- Total
Zeta Oph's Study
퍼셉트론과 신경망 - 딥러닝 공부 (1) 본문
앞으로 여러 글에 걸쳐 딥러닝 기초를 공부해보려고 합니다. 이 글에서는 신경망이란 무엇인지 알아보도록 하겠습니다.
신경망이란?
신경망(Neural Network)이란 인간의 뉴런 구조를 본떠 만든 기계학습 모델입니다.
우리 뇌는 뉴런이라는 신경 세포들에 의해 작동되는데, 뉴런들은 서로 연결되어 신호를 주고 받습니다. 만약 어떤 뉴런에 들어온 신호의 총합이 일정 값을 넘지 않는다면 신호를 다른 뉴런으로 내보내지 않지만, 일정 값을 넘는다면 신호를 내보내는 방식으로 작동합니다.
신경망도 마찬가지 입니다. 각 뉴런(노드)별로 입력 신호가 있고, 입력 신호를 판단하여 출력 신호를 내보냅니다. 이러한 구조를 한 층에 여러개를 놓고, 그러한 층을 또 여러 층을 쌓은 것이 신경망입니다.
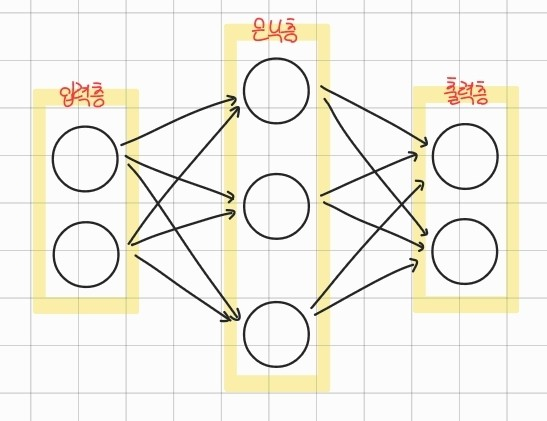
위 그림은 3층 신경망을 나타낸 것입니다. (실제로는 노드의 개수가 그림처럼 적지도 않고, 층의 개수도 훨씬 많습니다.) 층을 하나하나 살펴봅시다. 먼저 입력층은 입력 신호를 받는 층입니다. 출력층은 출력 신호를 내보내는 역할을 하는 층이고, 입력층과 출력층 사이 숨겨져 있는 층을 은닉층이라고 합니다.
그런데 사실 신경망이 등장하기 전에 인간의 뇌 구조를 본뜬다는 같은 아이디어를 바탕으로 등장한 것이 있습니다. 바로 퍼셉트론(perceptron)입니다.
퍼셉트론은 다수의 값을 입력받아 하나의 값을 출력하는 체계입니다. 아래 그림과 같이, 다수의 입력이 주어지면 이들의 합을 계산하여 임계치를 넘으면 출력하고 넘지 않으면 출력하지 않는 방식이죠. 또한 각 신호마다 가중치가 존재하여, 이를 고려한 입력신호를 받게 됩니다. 가중치 말고도 편향이라는 것이 존재합니다. 편향은 뉴런이 얼마나 쉽게 활성화되느냐를 제어하는 값입니다.

여기서 입력 신호 값$a$는 아래와 같이 계산합니다.
$$a=b+w_1x_1+w_2x_2=b+\sum{w_ix_i}$$
그리고 임계값 $\theta$를 넘을 경우 신호를 내보내고 그렇지 않을 경우 내보내지 않는 것은 아래와 같이 표현할 수 있습니다.
$$y=h(a)=\begin{cases}0\quad(b+w_1x_1+w_2x_2\leq\theta)\\1\quad(b+w_1x_1+w_2x_2\geq\theta)\end{cases}$$
신경망은 이러한 퍼셉트론들이 여러 층으로 쌓여 있는 것이라고 생각하시면 편합니다.
그런데 저 $h(x)$라는 함수는 뭘 까요? $h(x)$는 활성화 함수입니다. 활성화 함수는 입력 신호의 총합을 출력 신호로 바꾸어주는 역할을 합니다. 신경망에서 이용되는 활성화 함수에는 여러 종류가 있는데, 몇 가지 알아보도록 합시다.
(1) Sigmoid 함수
시그모이드 함수는 아래와 같은 식으로 표현되는 함수로, 그래프는 아래와 같이 생겼습니다.
$$h(x)=\frac{1}{1+e^{-x}}$$

(2) 계단 함수
계단 함수는 가장 간단한 형태의 활성화 함수라고 할 수 있습니다. 입력이 0보다 작으면 0을, 0보다 크면 1을 출력합니다.

(3) ReLU 함수
오래 전부터 쓰여온 활성화 함수가 시그모이드 함수라면, ReLU 함수는 최근에 많이 이용되는 함수입니다. 입력이 0 이하이면 0을 출력하고, 0 이상이면 입력값을 그대로 출력하는 함수로, 그래프는 아래와 같이 생겼습니다.

이외에도 다양한 활성화 함수가 있을 수 있지만, 모두 공통적인 특징을 가지고 있습니다. 바로 비선형 함수라는 것입니다. 신경망에서 활성화 함수는 비선형 함수를 사용합니다. 그 이유는 선형 함수를 사용하게 된다면 층을 쌓는 의미가 없어지기 때문입니다. 여기서 퍼셉트론 대신 신경망을 사용하는 이유가 있습니다. 퍼셉트론은 뉴런이 하나만 있기 때문에 한계가 있습니다. 예를 들어, 논리 게이트 중에 XOR 게이트라는 것이 있습니다. 두 값이 서로 같으면 0, 다르면 1을 반환하는 게이트인데, XOR 게이트를 퍼셉트론 하나로 구현할 수 있을까요? 즉, 직선 하나를 그어 아래와 같은 점들을 분류할 수 있을까요?

여러번 직선을 긋다보면 알겠지만, 불가능하다는 것을 알 수 있습니다. 즉, 선형 함수로는 해결 불가능한 분류 문제가 존재합니다. 하지만 만약 직선으로 국한되지 않는다면 아래와 같이 곡선을 그어 해결할 수 있겠죠. 이를 통해 비선형의 활성화 함수를 사용하여 "곡선을 그릴 수 있도록"하는 것입니다.

이러한 효과를 얻기 위해 활성화 함수로 비선형 함수를 사용하는 것입니다.
이 퍼셉트론들을 여러개, 여러층 쌓은 것이 신경망이라고 하였습니다. 퍼셉트론을 한 층에 여러개 놓을 수록 다음 층의 입력 변수가 다양해진다는 것이고, 여러 층을 쌓을 수록 비선형 함수를 더 많이 합성한다는 것입니다. 이를 통해, 노드의 수가 많을 수록, 은닉층을 많이 쌓을수록 대체적으로 신경망이 복잡한 문제도 해결할 수 있게 된다는 것을, 즉 성능이 좋아진다는 것을 의미한다고 할 수 있습니다. 아래는 3층 신경망, 즉 가중치 층이 3개인 신경망을 나타낸 그림입니다.

그림을 보시면, 출력층에 또 새로운 함수 $\sigma(x)$가 있습니다. 이 함수의 역할은 무엇일까요?
기계학습 문제는 크게 분류(classification)과 회귀(regression)으로 나뉩니다. 분류는 입력 데이터를 통해 데이터가 어느 클래스에 속하는지를 파악하는 문제이고, 회귀는 입력 데이터를 바탕으로 (연속적인) 수치를 예측하는 문제입니다. 출력층의 함수 $sigma(x)$는 분류 문제인지 회귀 문제인지에 따라 달라집니다.
일반적으로 회귀에는 항등함수를 사용합니다. 항등함수는 입력값을 그대로 출력하는 함수입니다. 즉 $\sigma(x)=x$입니다.
분류 문제에서는 소프트맥스 함수(softmax function)을 많이 사용합니다. 소프트맥스 함수의 식은 아래와 같습니다.
$$y_k=\frac{\mbox{exp}(a_k)}{\sum_{i=1}^n \mbox{exp}(a_i)}$$
여기서 $n$은 출력층의 뉴런 수, $a_k$, $y_k$는 각각 그 중 $k$번째 입/출력을 뜻합니다.
소프트맥스 함수의 특징으로는, 출력값이 0에서 1 사이이고, 총합이 1이라는 것입니다. 이 특징으로부터 소프트맥스 함수를 왜 분류 문제에 사용하는지 추론해볼 수 있습니다. 분류 결과를 소프트맥스 함수의 출력값으로 이용한다는 것은, 출력값이 입력값이 나타내는 것이 그 클래스일 확률을 의미한다고 생각할 수 있습니다. 예를 들어, $y_0=0.18$이라는 것은 답이 0번째 클래스일 확률이 0.18이라는 것을 의마한다고 볼 수 있는 것이죠. 그래서 보통 출력층의 노드 수는 분류 문제라면 클래수 수, 회귀 문제라면 도출해야하는 연속적인 값의 수로 설정합니다.
이렇게 딥러닝 공부 첫 번째 글에서는 퍼셉트론과 신경망이 무엇인지 간단하게 살펴보았습니다. 다음 글에서는 이 신경망을 구현하고, 학습하는 것을 차례대로 다루어 보도록 하겠습니다.
참고 : 밑바닥부터 시작하는 딥러닝
'프로그래밍' 카테고리의 다른 글
| 신경망의 학습(이론편) - 딥러닝 공부 (3) (1) | 2023.06.05 |
|---|---|
| 신경망의 구현 - 딥러닝 공부 (2) (1) | 2023.05.31 |
| 다항 회귀 (Polynomial Regression) (2) | 2023.05.16 |
| (연립) 미분 방정식의 수치적 해법 (2) : 룽게-쿠타 방법(Runge-Kutta Method)과 로트카-볼테라 방정식(Lotka-Volterra Equation) (1) | 2023.04.01 |
| 미분 방정식의 수치적 해법 (1) : 오일러 방법(Euler's Method)과 종단속력(Terminal Velocity) (1) | 2023.04.01 |




