| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- java
- 회로이론
- 신경망
- 벡터 해석
- 최단 경로
- 딕셔너리
- Asteroid RL
- 계단 오르기
- 파이썬
- 강화학습
- 자료형
- 이진탐색트리
- 피보나치 수열
- 2P1L
- Python
- cURL
- BST
- 소행성
- 선적분
- 딥러닝
- 델
- Class
- 벡터해석
- 미분 방정식
- 코드업
- 함수
- 자바
- auto-encoder
- 백트래킹
- dictionary
- Today
- Total
Zeta Oph's Study
신경망의 학습(이론편) - 딥러닝 공부 (3) 본문
이 글에서는 신경망을 학습하는 방법에 대해 알아보도록 하겠습니다.
저번 글에서 신경망을 구현해보았습니다.
https://crane206265.tistory.com/18
신경망의 구현 - 딥러닝 공부 (2)
이 글에서는 저번 글에 이어 신경망을 구현해보도록 하겠습니다. 저번 글에서 퍼셉트론이 무엇인지, 신경망이 무엇인지, 그리고 이를 이해하기 위해 필요한 기초 지식들을 다루었습니다. https://
crane206265.tistory.com
신경망을 구현해보았는데, 우리가 만든 신경망은 아직 가중치와 편향과 같은 값을 직접 정해주어야 합니다. 즉, 아직 연산만 가능하고 학습은 하지 못합니다. 이번 글에서는 그 "학습"에 대해 알아보려고 합니다.
신경망 학습이란, 데이터로부터 매개변수의 값 (가중치, 편향 등)을 정하는 과정입니다. 데이터로부터 특징을 추출해서, 규칙을 발견하고 발견한 규칙으로 결과를 예상해본다는 과정은 기계학습과 신경망이 같습니다. 다만 둘의 차이는, 기계학습은 데이터로부터 특징을 추출하는 작업까지는 사람이 해주어야 하고, 규칙을 발견하고 발견한 규칙으로 결과를 예상하는 것을 기계가 하는데, 신경망은 이 모든 작업을 컴퓨터 스스로 수행한다는 것이죠.
이 데이터라는 것이 많을 수록, 당연히 더 잘 학습될 것입니다. 그런데, 아래 그림 2개 중 어떤 것이 더 잘 학습된 것으로 보이나요?
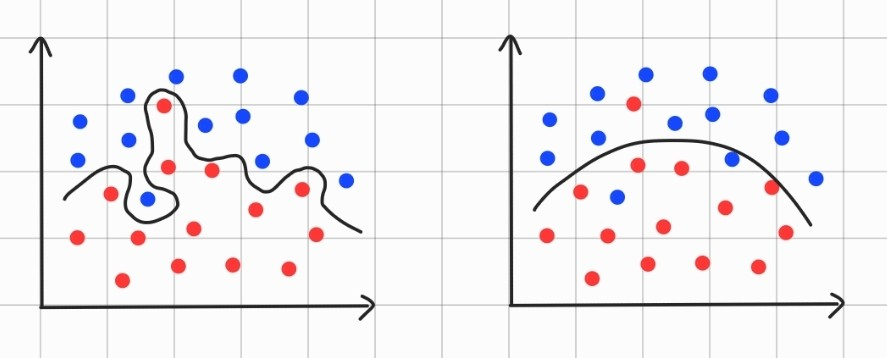
왼쪽 그림이 학습을 할 때 사용한 데이터를 완벽하게 예측하긴 하지만.... 과연 학습에 사용하지 않은, 새로운 데이터가 들어왔을 때 잘 예측할 수 있을까요? 그렇다고 말하긴 힘들 것입니다. 이렇게, 데이터를 과하게 학습하여 학습에 사용된 데이터만 예측하고, 새로운 데이터는 잘 예측하지 못 하는 왼쪽 그림과 같은 상태를 과적합(overfitting)이라고 합니다. 이 과적합을 방지하기 위해, 보통 신경망을 학습시킬 때 데이터를 2개로 나눕니다. 훈련에 사용할 데이터, 그리고 학습이 끝난 후 성능을 테스트 하는데 사용할 데이터 2개로 말이죠.
자, 본격적으로 학습을 진행하는 방법에 대해 알아봅시다. 데이터를 잘 예측하도록 학습이 되는 것이 우리의 목표입니다. 즉, 잘 학습이 되었다면 예측한 것과 답의 오차가 작을 것입니다. 이러한 아이디어를 기반으로, 손실 함수(loss funtion)라는 것을 최소화 하는 방향으로 학습한다는 것이 신경망 학습의 핵심이라고 할 수 있습니다. 손실 함수는 추정값과 정답 사이의 오차의 크기를 나타내는 함수인데, 당연히 손실 함수가 작을 수록 오차가 작아지는 것이므로 예측을 잘 한다고 할 수 있을 것입니다. 그러면 손실 함수의 종류에 대해 알아보도록 하겠습니다.
(1) 평균 제곱 오차(Mean Squared Error, MSE)
평균 제곱 오차는 아래와 같은 식으로 주어집니다.
$$MSE = \frac{1}{2}\sum_k (y_k-t_k)^2$$
여기서 $y_k, t_k$는 각각 추정값과 정답을 의미합니다.
추정값에서 정답을 뺀 값인 오차를 모두 더한다는 의미인데, 오차가 음수일 수도 있고 양수일 수도 있으니 제곱을 해서 더해줍니다. 꼭 그렇지 않아도 되지만, 앞에 1/2이 붙는 이유는 나중에 경사 하강을 위해 미분을 하면 2가 튀어나오기 때문에 그것을 없애주기 위함입니다.
(2) 교차 엔트로피 오차(Cross Entropy Error, CEE)
교차 엔트로피 오차는 아래와 같은 식으로 주어집니다.
$$CEE=-\sum_k t_k \mathrm{ln}y_k$$
마찬가지로 $y_k, t_k$는 각각 추정값과 정답을 의미합니다.
그런데, $y_k$가 0이면 로그는 계산이 불가합니다. 따라서 이를 방지하기 위해, $\delta=10^{-7}$과 같은 매우 작은 값을 더해주고 계산합니다.
또한 원-핫 인코딩을 사용하는 경우에는, 정답이 아니면 $t_k=0$이므로 정답인 경우만 계산해주어도 된다는 편리함이 있습니다. 이때 원-핫 인코딩은 정답 데이터를 설정하는 방법으로, 정답인 경우에는 1, 나머지는 0을 저장하는 방법입니다.
위 식들은 각각의 배치에 대해서 계산할 수 있는 식이고, 그러한 배치가 N개 있다고 하면, 각각의 loss function을 $E$라고 하였을 때 전체 loss funtion은 아래와 같이 주어진다는 것을 생각할 수 있습니다.
$$loss function=\frac{1}{N}\sum_nE_n$$
여기서 조금씩 가져오는 배치를 mini-batch라고 합니다. 데이터 일부를 사용하여 전체에 대한 근사치를 구한다는 것이죠.
그런데, 학습 지표로 정확도를 놔두고 이러한 손실 함수를 사용하는 이유가 무엇일까요? 그 이유는, 곧 설명하겠지만 매개변수를 갱신하는 과정에서 미분이 이용되는데, 정확도는 대부분의 점에서 미분하여 0이 되기 때문입니다. 즉, 미소 변화를 주어 매개변수를 조금씩 갱신시키려고 하는데, 미소 변화로 반응을 거의 하지 않습니다. 그렇기 때문에 미소 변화에도 반응이 큰 손실 함수를 학습 지표로 사용하는 것입니다.
이제 손실 함수를 최소화 시키는 방법인 경사 하강법(gradient descent)에 대해 알아보도록 하겠습니다. 경사 하강법은 어떤 함수의 극솟값을 찾는 방법으로서, 함수 $f$의 극솟값을 찾고 싶으면 아래 식을 반복하여 계산해주면 됩니다.
$$\mathbf{x_{i+1}}=\mathbf{x_i}-\eta\mathbf{\nabla}f$$
여기서 $\eta$는 학습률(learning rate)입니다. 경사 하강법을 그래프로 그려보면 극소 방향으로 조금씩 움직이는 모양으로 나타나는데, 여기서 한 번 움직임의 크기가 학습률이라고 생각하시면 될 것 같습니다. 학습률은 사람이 직접 설정해주어야 하는 하이퍼파라미터(hyperparameter)인데, 학습률을 너무 작게 설정하면 학습이 잘 진행되지 않고, 너무 크게 설정하면 극솟값을 찾지 못하고 발산해버릴 수 있습니다.
경사 하강법을 이용해 손실 함수의 극솟점을 찾으면, 그리고 극솟점을 찾는 과정에서 가중치와 편향 등 값을 갱신시켜주면, 그것이 학습이라고 할 수 있습니다.
$$W=\begin{bmatrix} w_{11} & w_{21} & w_{31} \\ w_{12} & w_{22} & w_{32} \\ \end{bmatrix}$$
위와 같은 가중치 행렬 $W$가 있을 때, 손실함수 $f$를 가중치 행렬 $W$로 편미분 해주어 경사하강을 실행해주는 것입니다. 아래와 같이 말이죠.
$$\frac{\partial f}{\partial W}=\begin{bmatrix} \frac{\partial f}{\partial w_{11}} & \frac{\partial f}{\partial w_{21}} & \frac{\partial f}{\partial w_{31}} \\ \frac{\partial f}{\partial w_{12}} & \frac{\partial f}{\partial w_{22}} & \frac{\partial f}{\partial w_{32}} \\ \end{bmatrix}$$
즉, 각 가중치 값마다 경사 하강법을 실행하여 가중치 각각을 최적화시키는 겁니다.
총 정리를 해봅시다. 신경망을 학습하는 알고리즘은 아래와 같습니다.
1. mini batch를 무작위로 가져오기
2. 가져온 mini batch를 이용하여 손실 함수의 기울기 계산
3. 매개변수 갱신
위의 1~3 과정이 반복되며 학습이 진행되는 것입니다. 이때 mini batch를 무작위로 가져온다고 하여 이 방법을 확률적 경사 하강법(Stochastic Gradient Descent, SGD)라고 부릅니다.
이렇게 확률적 경사 하강법을 이용한 신경망의 학습 방법에 대해 알아보았습니다. 다음 글에서는 이 글의 내용을 바탕으로 신경망의 학습을 구현해보도록 하겠습니다.
'프로그래밍' 카테고리의 다른 글
| [천문 + 프로그래밍] Missing Star 생성기 (1) | 2023.08.20 |
|---|---|
| 다익스트라 알고리즘(Dijkstra Algorithm) (1) | 2023.07.11 |
| 신경망의 구현 - 딥러닝 공부 (2) (1) | 2023.05.31 |
| 퍼셉트론과 신경망 - 딥러닝 공부 (1) (1) | 2023.05.31 |
| 다항 회귀 (Polynomial Regression) (2) | 2023.05.16 |




