| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- auto-encoder
- 피보나치 수열
- 신경망
- 이진탐색트리
- 계단 오르기
- 함수
- 선적분
- 소행성
- 강화학습
- 자바
- dictionary
- 벡터 해석
- 파이썬
- 자료형
- 미분 방정식
- 코드업
- 벡터해석
- 최단 경로
- 딕셔너리
- Asteroid RL
- 딥러닝
- 2P1L
- BST
- 델
- cURL
- Python
- 백트래킹
- 회로이론
- Class
- java
- Today
- Total
Zeta Oph's Study
[Asteroid RL] 배경 이론 - 람베르트 코사인 법칙, 구면 좌표계 본문
https://crane206265.tistory.com/44
[Asteroid RL] 프로젝트 소개
언젠가 천문학과 인공지능을 융합해보고 싶었습니다. 문득 멍 때리다가, 평소에 관심을 가지고 있던 태양계 소천체 분야와 강화학습을 융합할 주제가 떠올랐습니다. 그래서 Asteroid RL 프로젝트
crane206265.tistory.com
지난 글에서 Asteroid RL 프로젝트에 대해 소개했었습니다.
프로젝트를 본격적으로 진행하기 전에, 배경이론 몇가지를 먼저 소개하려고 합니다.
프로젝트가 진행되면서 배경이론이 더 추가될 수도 있지만, 우선 가장 필수적이고 기본적인 것을 다루어 보겠습니다.
람베르트 코사인 법칙 (Lambert's Cosine Law)
람베르트 코사인 법칙은, 입사하는 빛의 각도와 반사되는 빛의 양에 대한 관계를 나타내는 법칙입니다. (정확히는 램버시안 반사율을 가지는 램버시안 표면에 적용되는 법칙이지만, 대충 이상적인 반사가 일어나는 표면이라고 생각하시면 될 것 같습니다.)

입사되는 빛의 양이 $I_0$이고, 입사각이 $\theta$이면, 반사되는 빛의 양 $I$는 입사각의 코사인 값에 비례합니다. 즉,
$$I=I_0\cos{\theta}$$
로 쓸 수 있습니다. 쉽게 생각하면, 빛이 수직으로 입사하면 반사되는 양도 많아지고, 거울이 기울어져있을수록 반사되어 눈에 들어오는 양이 적어진다는 것이죠.
소행성의 광도곡선으로 소행성의 모양을 파악할 수 있는 가장 핵심이 바로 이 람베르트 코사인 법칙입니다. 소행성의 울퉁불퉁한 표면이 람베르트 코사인 법칙에 따라 반사하는 빛의 양이 계속 변하게 만들고, 이를 통해 소행성의 광도곡선이 특징적으로 나타나는 것이죠.
구면 좌표계 (Spherical Coordinate)
우리가 평소에 많이 쓰는 좌표계는 직교좌표계입니다. 3차원에서 $(x, y, z)$로 점의 위치를 나타내죠.
구면 좌표계는 $(r, \theta, \phi)$로 좌표를 나타냅니다. $r$은 원점으로부터의 거리, $\theta, \phi$는 각각 방위각, 천정각입니다.
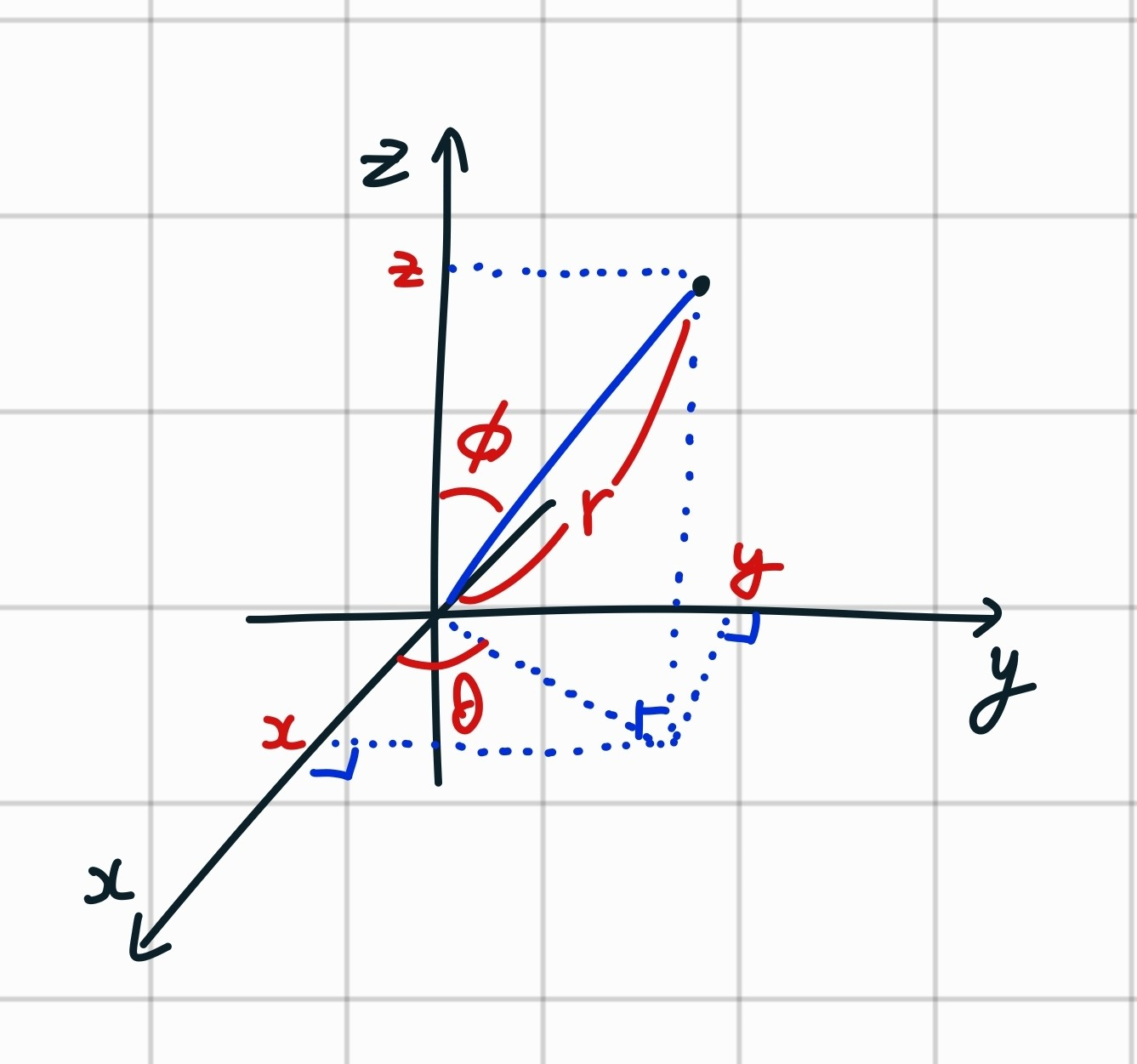
구면 좌표계에서 직교 좌표계로의 변환은 아래와 같이 할 수 있습니다.
$$\begin{cases} x=r\cos{\theta}\sin{\phi} \\ y=r\sin{\theta}\sin{\phi} \\ z=r\cos{\phi} \end{cases}$$
반대로 직교 좌표계에서 구면 좌표계로의 변환은
$$\begin{cases} r=\sqrt{x^2+y^2+z^2} \\ \theta=\arctan2(y, x) \\ \phi=\arctan2(\sqrt{x^2+y^2}, z) \\ \end{cases}$$
여기서 $\arctan2(a, b)$는 좌표평면에서 $(a, b)$의 $x$축 양의 방향으로 잰 각도를 결과값으로 주는 함수입니다.
구면 좌표계는 특정한 상황에서 매우 편리하게 쓰일 수 있습니다. 지구 같은 경우, 어떤 도시의 좌표를 $(x, y, z)$로 나타내는 것보다 위도 경도를 이용하는게 더 편리하듯 말이죠. 소행성의 모양을 나타내는 경우 또한 구면 좌표계를 사용하면 편리할 것 같아 이 프로젝트에서 구면 좌표계를 사용하게 되었습니다.
하지만 벡터의 내적/외적의 경우는 직교 좌표계에서 훨씬 간단하게 계산될 수 있습니다. 따라서 이 프로젝트에서 그러한 연산이 필요한 경우, 직교 좌표계로 바꾸어 연산을 해준 후 다시 구면 좌표계로 되돌리는 방식을 따르려 합니다.
이렇게 Asteroid RL 프로젝트에서 사용할 몇 가지 기본 개념을 소개하였습니다. 프로젝트를 위한 개념 설명글이기 때문에 유도나 자세한 설명은 생략하였습니다. 다음 글에서는 소행성 모형을 설계하는 것을 다루어보겠습니다.
'개인 연구 > Asteroid AI' 카테고리의 다른 글
| [Asteroid AI] Asteroid Modeling : Basic Structure (3) | 2024.10.26 |
|---|---|
| [Asteroid RL] 프로젝트 소개 (2) | 2023.09.30 |


