| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 신경망
- 피보나치 수열
- 자바
- Asteroid RL
- java
- BST
- Class
- Python
- 이진탐색트리
- 함수
- 파이썬
- 미분 방정식
- 델
- 선적분
- cURL
- auto-encoder
- 2P1L
- 코드업
- 회로이론
- dictionary
- 계단 오르기
- 소행성
- 강화학습
- 자료형
- 딥러닝
- 최단 경로
- 딕셔너리
- 벡터해석
- 백트래킹
- 벡터 해석
- Today
- Total
Zeta Oph's Study
다익스트라 알고리즘(Dijkstra Algorithm) 본문
이 글에서는 다익스트라 알고리즘에 대해 소개해보도록 하겠습니다.
다익스트라 알고리즘(Dijkstra Algorithm)
다익스트라 알고리즘(Dijkstra Algorithm)은 최단 경로를 찾는 알고리즘 중 하나로, 네덜란드의 컴퓨터 과학자 에츠허르 다익스트라가 고안하였습니다. 다익스트라 알고리즘을 활용하면 한 노드와 다른 모든 노드들 간의 최단 경로를 찾을 수 있지만, 노드간 거리(가중치)가 하나라도 음수인 경우에는 사용할 수 없다는 조건이 있습니다.
다익스트라 알고리즘이 작동하는 과정에 대해서 알아보겠습니다.
먼저 사용하는 배열은 아래와 같습니다.
- 비용 배열 weight[i][j] = l : 노드 i에서 노드 j로 가는데 드는 비용이 l. 연결이 되어있지 않다면 거리를 무한대로 기록한다.
- 방문 노드 배열 visit[i] : 0 또는 1로 기록하여 노드 i를 방문하였는지 표시
- 시작점-노드 비용 배열 dist[i] : 시작 노드에서 노드 i까지 가는데 드는 비용 기록. 알고리즘을 실행하게 되면 이 dist 배열을 갱신하며 최단 경로를 찾게 된다.
다음은 알고리즘 작동 순서입니다.
(S가 시작 노드인 경우)
1. dist 배열을 weight 배열에 저장된 값을 이용하여 초기화한다.
dist[i] = weight[S][i]
2. 시작점을 방문 처리한다.
visit[S] = 1
3. 방문하지 않은 노드 중 dist 배열에서 최소비용노드(K)를 찾아 방문 처리한다.
4. 노드 K를 거쳐가는 것과 시작점에서 바로 가는 것의 비용을 비교한다. 만약 노드 K를 거쳐가는 것이 더 비용이 적다면 dist 배열을 그 값으로 갱신한다. 이때 방문한 노드는 4번 작업을 수행하지 않아도 된다.
if dist[i] > dist[K] + weight[K][i] : dist[i] = dist[K] + weight[K][i]
5. 모든 노드를 방문할 때까지 3, 4번 작업을 반복한다.
이를 순서도로 나타내보면 다음과 같습니다.

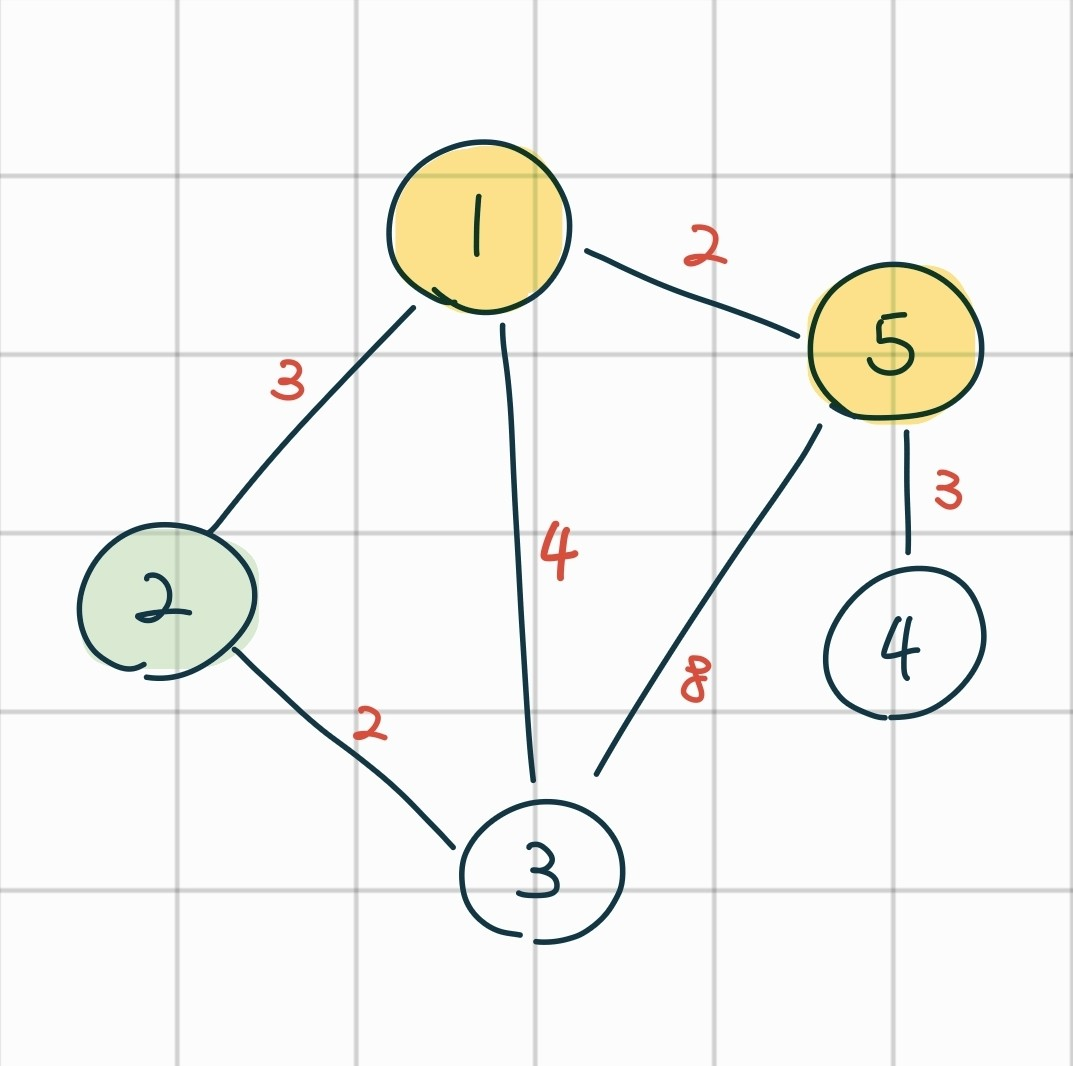
글과 순서도로만 설명하면 잘 와닿지 않을 수 있으니, 예시를 들어봅시다. 아래와 같은 그래프가 있다고 해봅시다.

위 그래프에서 시작 노드를 노드 1로 합시다. 노드 1을 방문처리 합니다.

맨 처음 배열의 상태는 아래와 같습니다.
| 노드 | 1 | 2 | 3 | 4 | 5 |
| visit | 1 | 0 | 0 | 0 | 0 |
| dist | 0 | 3 | 7 | INF | 2 |
dist 배열에서 최소 비용 노드는 5이므로, 노드 5를 방문합니다.

이제 노드 5를 거쳐가는 것과 1에서 바로 가는 것의 비용을 방문하지 않은 각 노드마다 비교해봅니다. 노드 4의 경우, dist 배열에 저장되어 있는 값은 INF지만 노드 5를 거쳐갈 경우 2+3=5로 비용이 더 작은 것을 알 수 있습니다. 따라서 노드 4의 dist 배열 값을 5로 갱신합니다.

| 노드 | 1 | 2 | 3 | 4 | 5 |
| visit | 1 | 0 | 0 | 0 | 1 |
| dist | 0 | 3 | 7 | 5 | 2 |
이제 다시 방문하지 않은 노드 중 dist 배열에서 최소 비용 노드를 찾습니다. 노드 2가 해당하므로, 노드 2를 방문합니다.
노드 2를 거쳐가는 것과 1에서 바로 가는 것의 비용을 방문하지 않은 각 노드마다 비교해봅니다. 이번 경우에는 모두 바로 가는 것이 더 비용이 적으므로, 아무 배열도 갱신하지 않습니다.
| 노드 | 1 | 2 | 3 | 4 | 5 |
| visit | 1 | 1 | 0 | 0 | 1 |
| dist | 0 | 3 | 7 | 5 | 2 |
...
이러한 방법으로 마지막까지 갱신하면 아래와 같이 최종 배열을 얻게 됩니다.
| 노드 | 1 | 2 | 3 | 4 | 5 |
| visit | 1 | 1 | 1 | 1 | 1 |
| dist | 0 | 3 | 7 | 5 | 2 |
여기서 dist 배열이 시작 노드(노드 1)부터 각 노드까지의 최단 경로의 길이입니다.
이렇게 다익스트라 알고리즘에 대해 알아보았습니다. 이 글에서 소개한 다익스트라 알고리즘은 에츠허르 다익스트라가 고안한 초기의 것이지만, 이후 우선순위 큐 등을 활용하여 개선된 다익스트라 알고리즘이 나오기도 하였습니다.
'프로그래밍' 카테고리의 다른 글
| [천문 + 프로그래밍] Missing Star 생성기 (1) | 2023.08.20 |
|---|---|
| 신경망의 학습(이론편) - 딥러닝 공부 (3) (1) | 2023.06.05 |
| 신경망의 구현 - 딥러닝 공부 (2) (1) | 2023.05.31 |
| 퍼셉트론과 신경망 - 딥러닝 공부 (1) (1) | 2023.05.31 |
| 다항 회귀 (Polynomial Regression) (2) | 2023.05.16 |




